OPENFOAM VALIDATION CASES
Taylor-Green Vortex
The Taylor–Green vortex solution is a classical case used for testing and validation of spatial and temporal accuracy of CFD solvers.
In 2D, the Taylor-Green vortex has the following analytical solution,
In this case, we solve the governing equations in a square domain with a length equal to \( 2 \pi \). The arbitrary constant \( k \) is equal to 1, and \( \rho \) and \( \nu \) are equal to 1. The simulation was run until reaching a physical time (t) equal to 0.3 seconds.
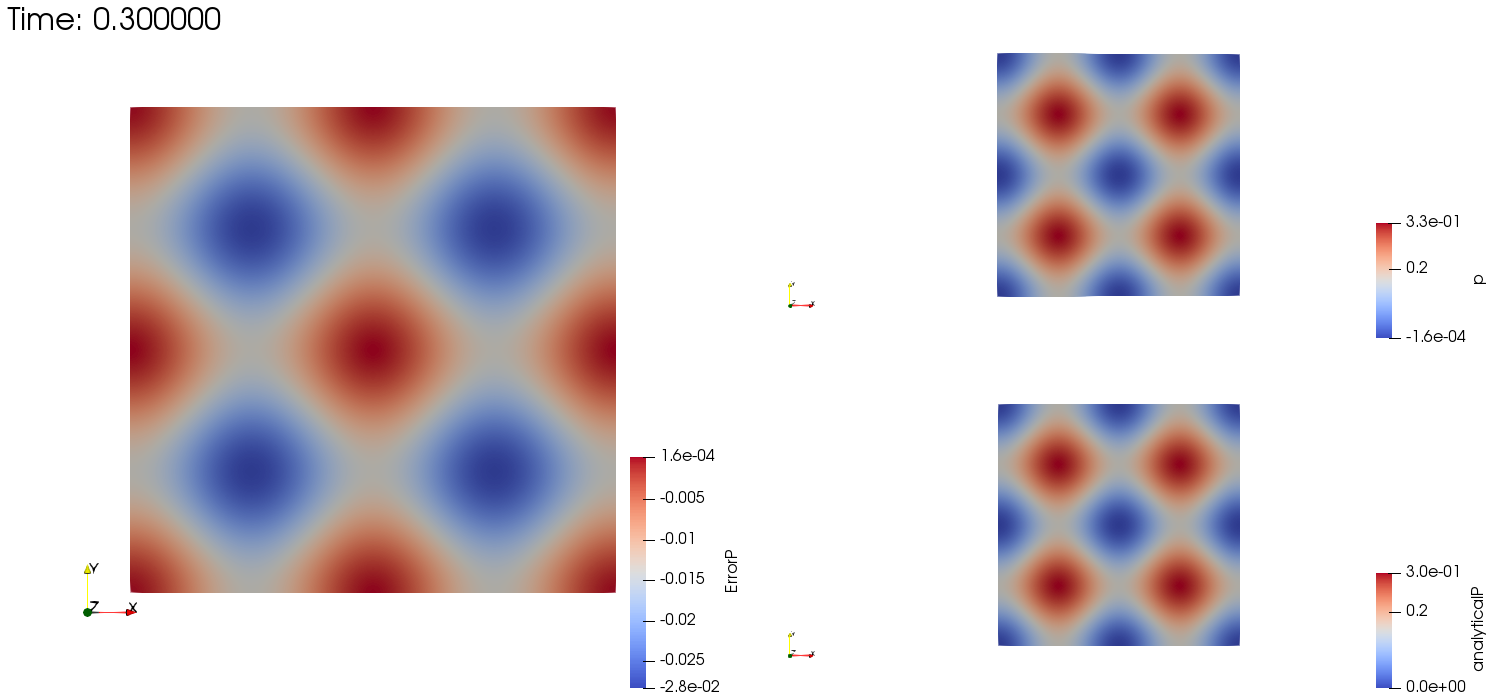 |
| Comparison of numerical and analytical solutions for pressure field (p). Left figure: error (p analytical - p numerical). Right figure: contours of pressure field (numerical and analytical). Physical time equal to 0.3 seconds. |
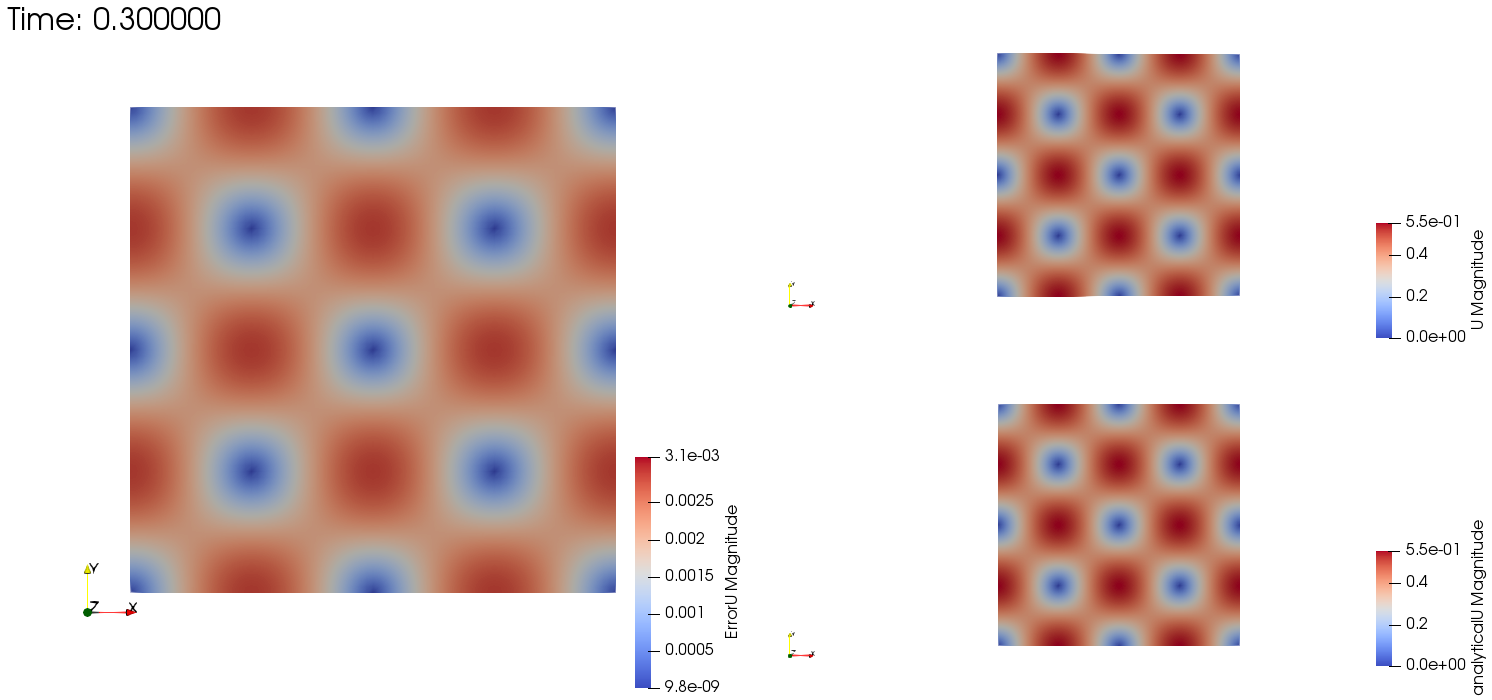 |
| Comparison of numerical and analytical solutions for velocity field (U). Left figure: error (U analytical - U numerical). Right figure: contours of velocity field (numerical and analytical). Physical time equal to 0.3 seconds. |
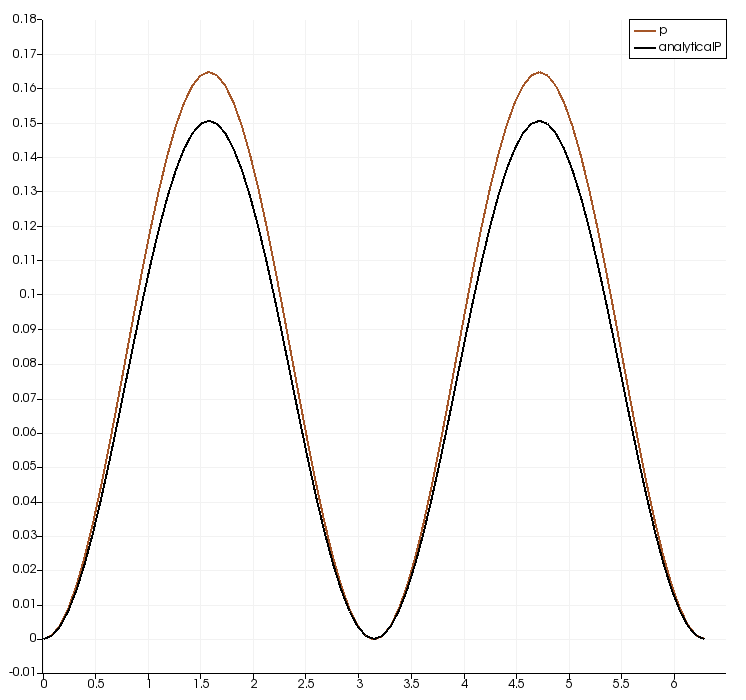 |
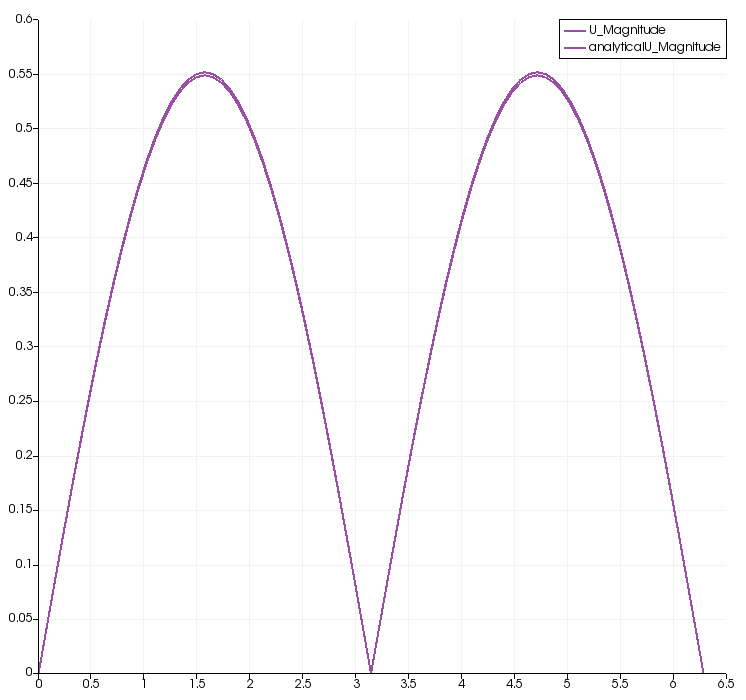 |
| Left figure: comparison of numerical and analytical solutions of pressure field. Right figure: comparison of numerical and analytical solutions of velocity field. The sampling was done in the left boundary (a vertical line). Physical time equal to 0.3 seconds. | |
References:
Taylor, G. I. and Green, A. E., Mechanism of the Production of Small Eddies from Large Ones, Proc. R. Soc. Lond. A, 158, 499–521 (1937).
Kim, J. and Moin, P., Application of a fractional-step method to incompressible Navier–Stokes equations, J. Comput. Phys., 59, 308–323 (1985).
Chorin, A. J., Numerical solution of the Navier–Stokes equations, Math. Comp., 22, 745–762 (1968).
